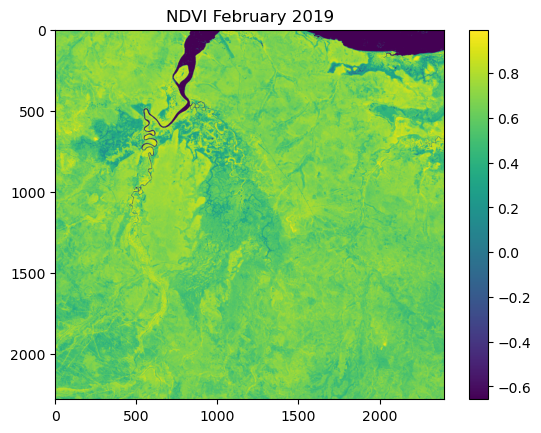
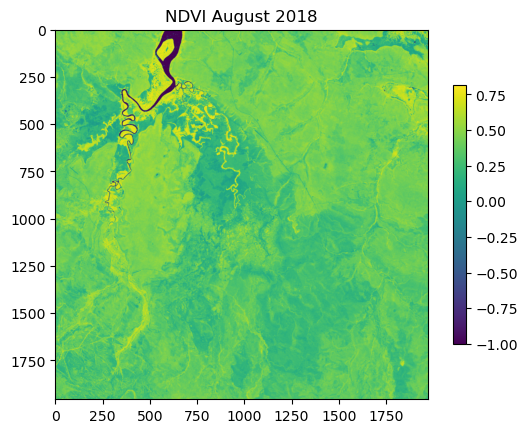
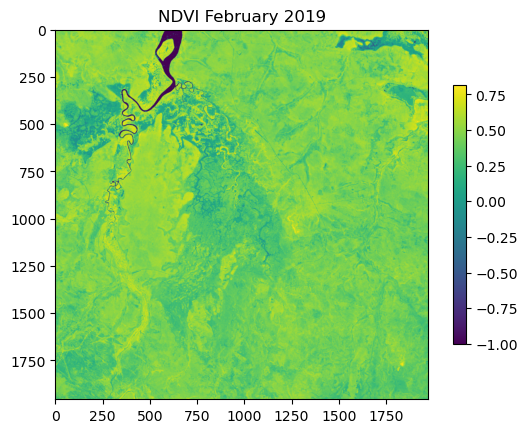
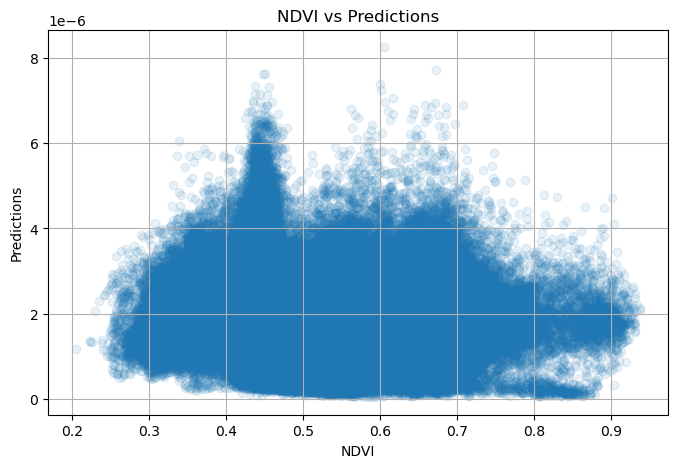
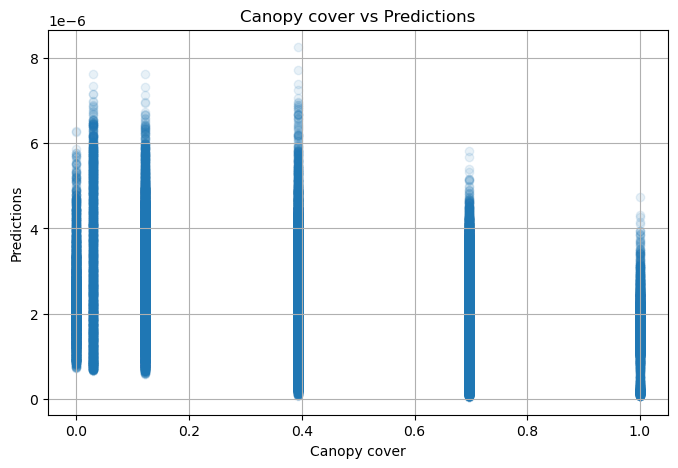
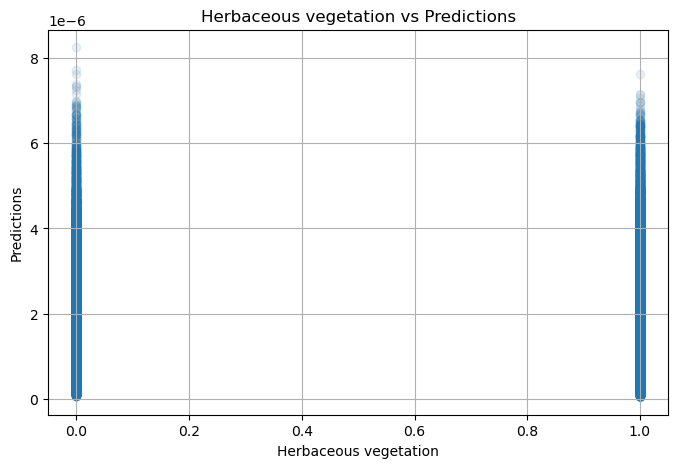
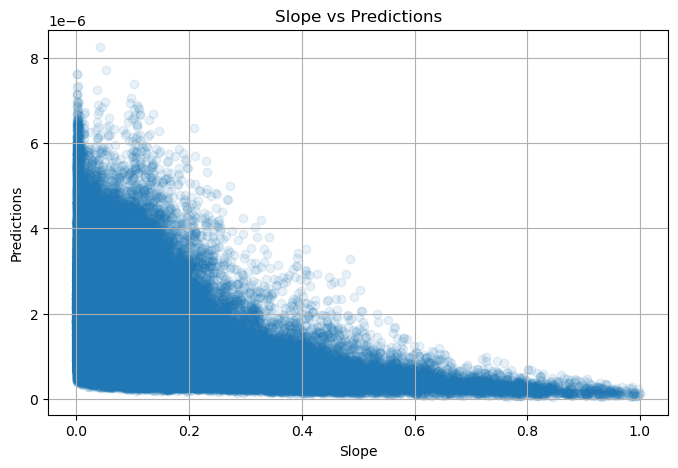
NDVI metadata:
{'driver': 'GTiff', 'dtype': 'float32', 'nodata': nan, 'width': 2400, 'height': 2280, 'count': 1, 'crs': CRS.from_wkt('PROJCS["GDA94 / Geoscience Australia Lambert",GEOGCS["GDA94",DATUM["Geocentric_Datum_of_Australia_1994",SPHEROID["GRS 1980",6378137,298.257222101,AUTHORITY["EPSG","7019"]],AUTHORITY["EPSG","6283"]],PRIMEM["Greenwich",0,AUTHORITY["EPSG","8901"]],UNIT["degree",0.0174532925199433,AUTHORITY["EPSG","9122"]],AUTHORITY["EPSG","4283"]],PROJECTION["Lambert_Conformal_Conic_2SP"],PARAMETER["latitude_of_origin",0],PARAMETER["central_meridian",134],PARAMETER["standard_parallel_1",-18],PARAMETER["standard_parallel_2",-36],PARAMETER["false_easting",0],PARAMETER["false_northing",0],UNIT["metre",1,AUTHORITY["EPSG","9001"]],AXIS["Easting",EAST],AXIS["Northing",NORTH],AUTHORITY["EPSG","3112"]]'), 'transform': Affine(25.0, 0.0, 0.0,
0.0, -25.0, -1406000.0)}
Affine transformation parameters:
| 25.00, 0.00, 0.00|
| 0.00,-25.00,-1406000.00|
| 0.00, 0.00, 1.00|
Shape of the raster:
(2280, 2400)