Dynamic SSF
Understanding and predicting animal movement is fundamental to ecology and conservation management. Models that estimate and then predict animal movement and habitat selection parameters underpin diverse conservation applications, from mitigating invasive species spread to enhancing landscape connectivity. However, many predictive models overlook fine-scale temporal dynamics within their predictions, despite animals often displaying fine-scale behavioural variability that might significantly alter their movement, habitat selection and distribution over time. Incorporating fine-scale temporal dynamics, such as circadian rhythms, within predictive models might reduce the averaging out of such behaviours, thereby enhancing our ability to make predictions in both the short and long term. We tested whether the inclusion of fine-scale temporal dynamics improved both fine-scale (hourly) and long-term (seasonal) spatial predictions for a significant invasive species of northern Australia, the water buffalo (Bubalus bubalis). Water buffalo require intensive management actions over vast, remote areas and display distinct circadian rhythms linked to habitat use. To inform management operations we generated hourly and dry season prediction maps by simulating trajectories from static and temporally dynamic step selection functions (SSFs) that were fitted to the GPS data of 13 water buffalo. We found that simulations generated from temporally dynamic models replicated the buffalo crepuscular movement patterns and dynamic habitat selection, resulting in more informative and accurate hourly predictions. Additionally, when the simulations were aggregated into long-term predictions, the dynamic models were more accurate and better able to highlight areas of concentrated habitat use that might indicate high-risk areas for environmental damage. Our findings emphasise the importance of incorporating fine-scale temporal dynamics in predictive models for species with clear dynamic behavioural patterns. By integrating temporally dynamic processes into animal movement trajectories, we demonstrate an approach that can enhance conservation management strategies and deepen our understanding of ecological and behavioural patterns across multiple timescales.
Description
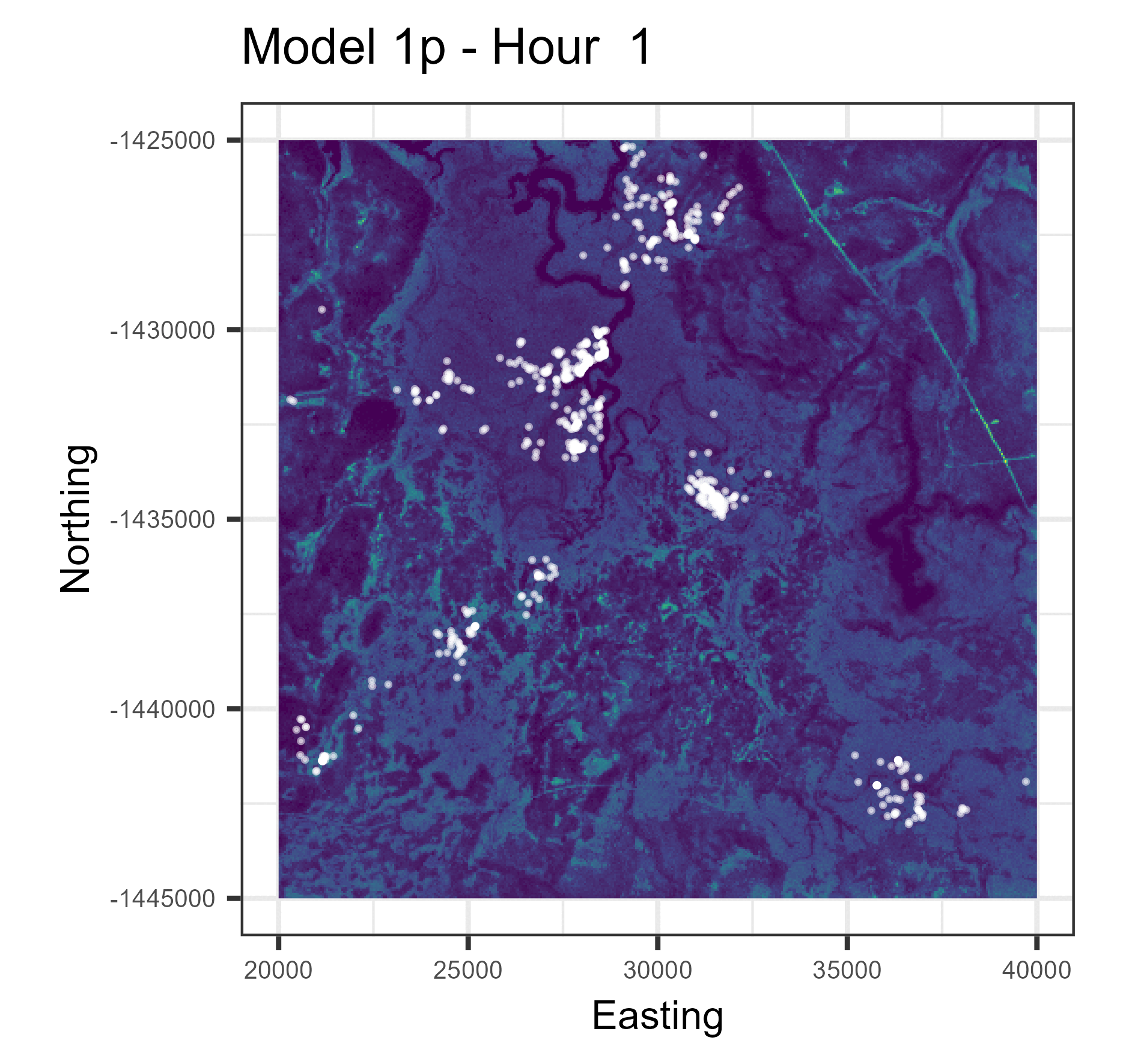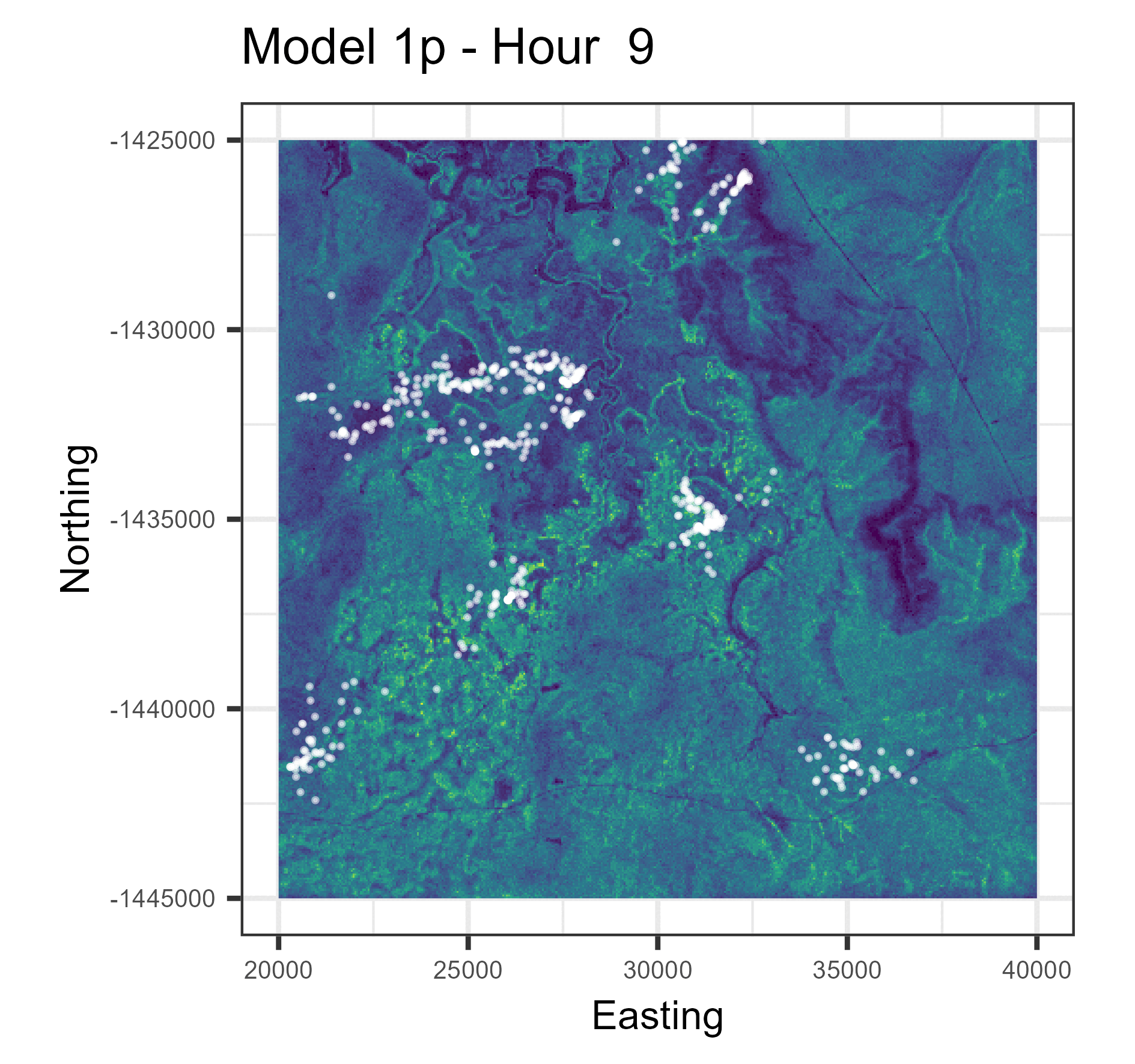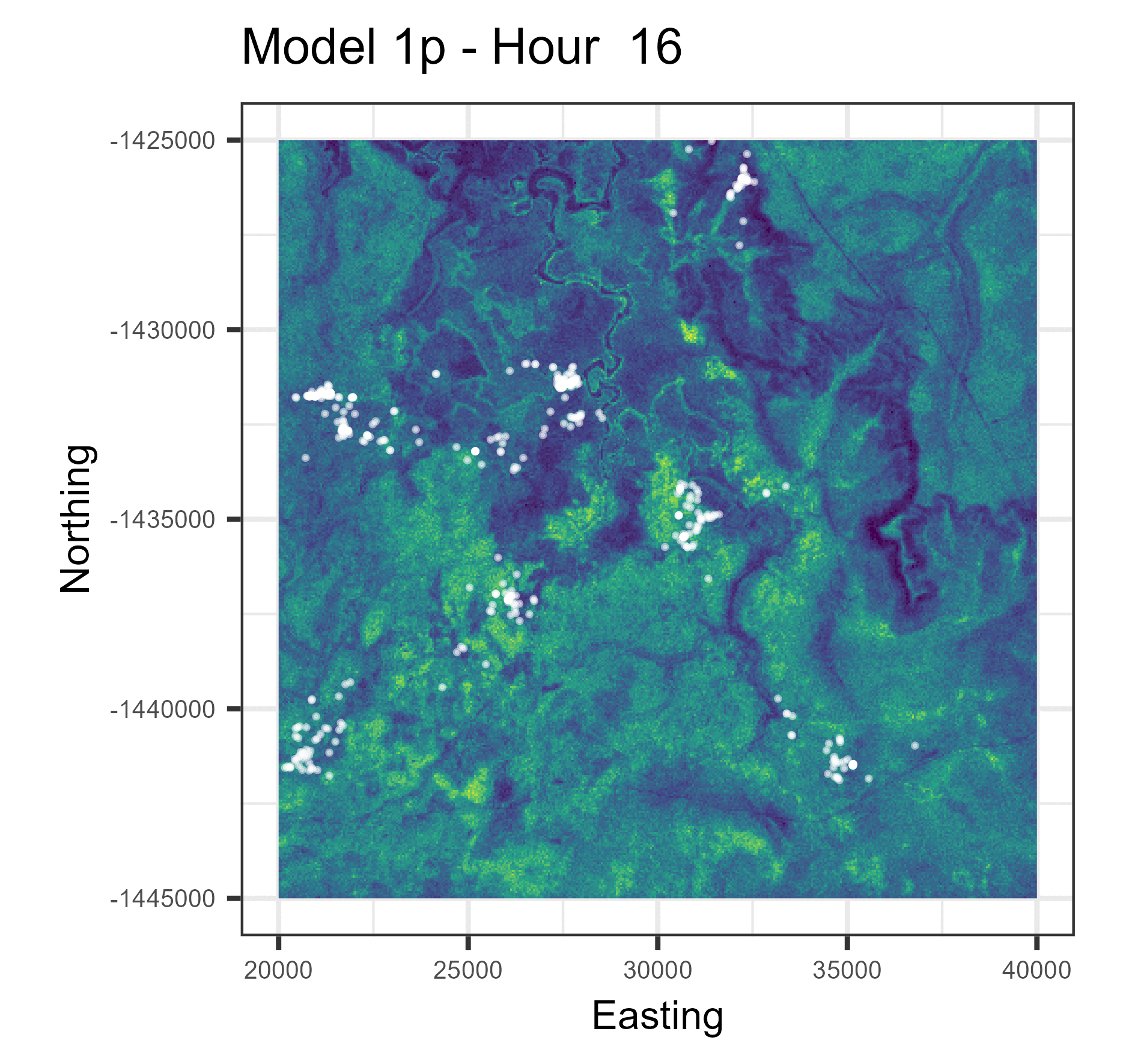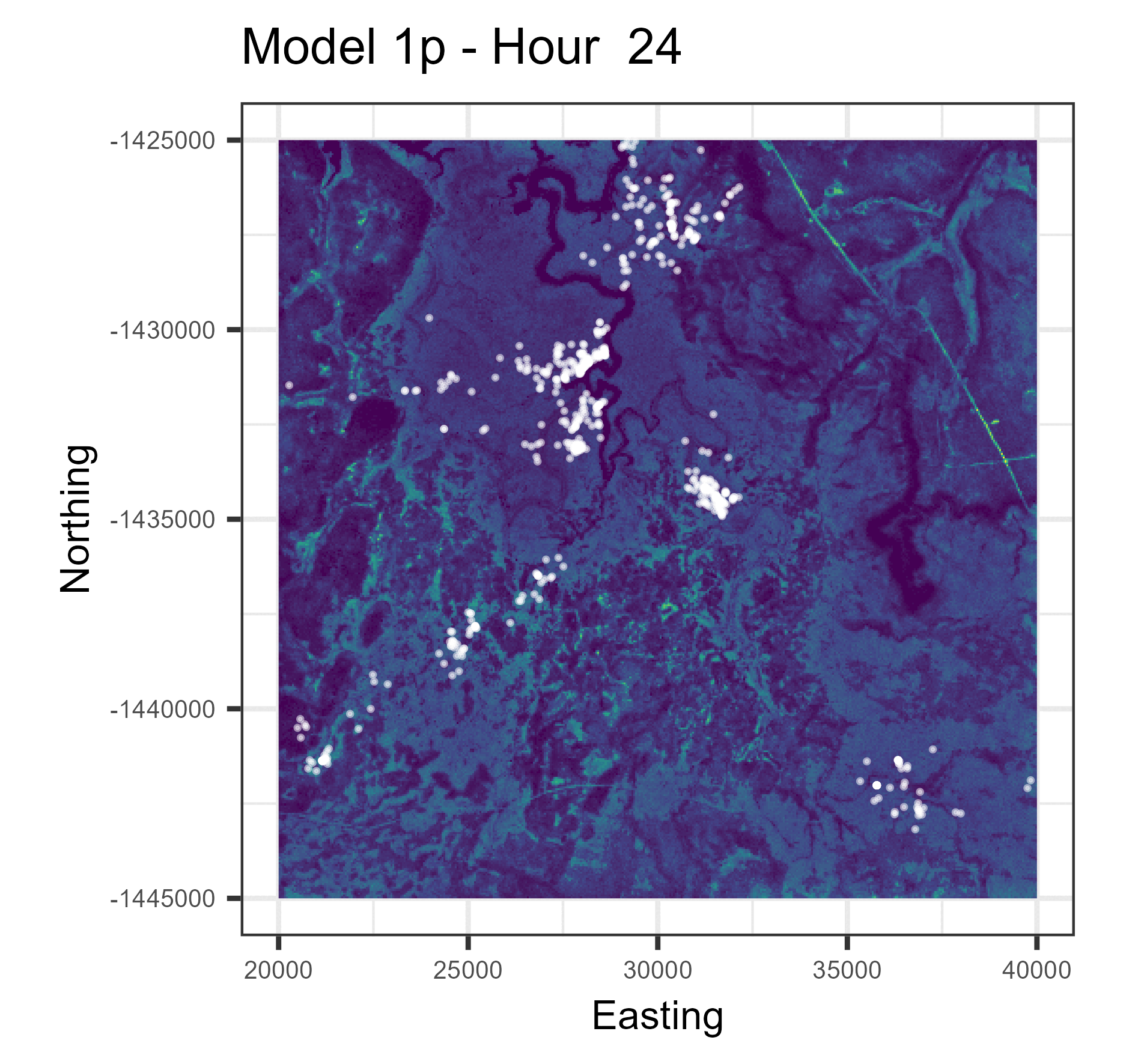
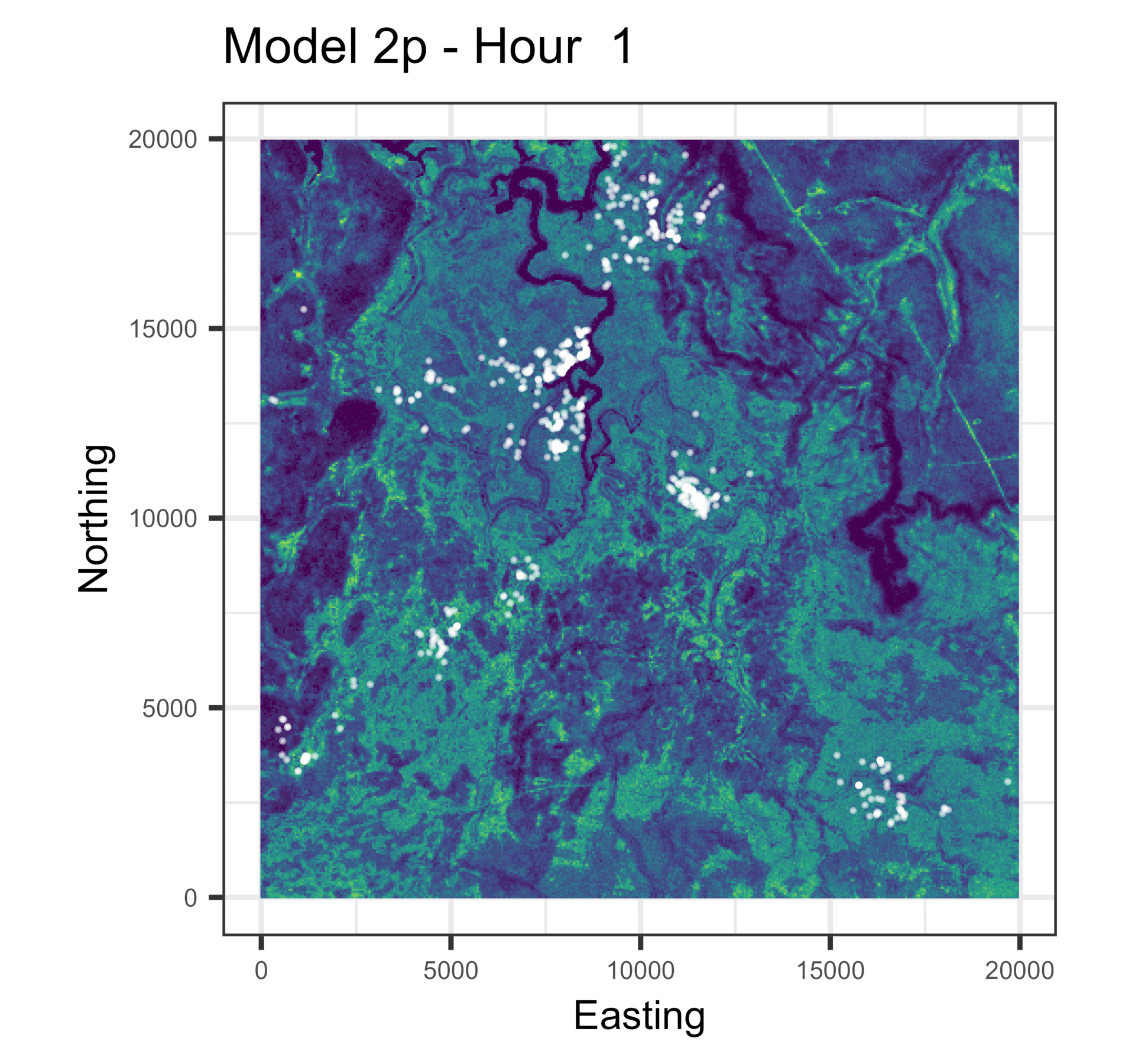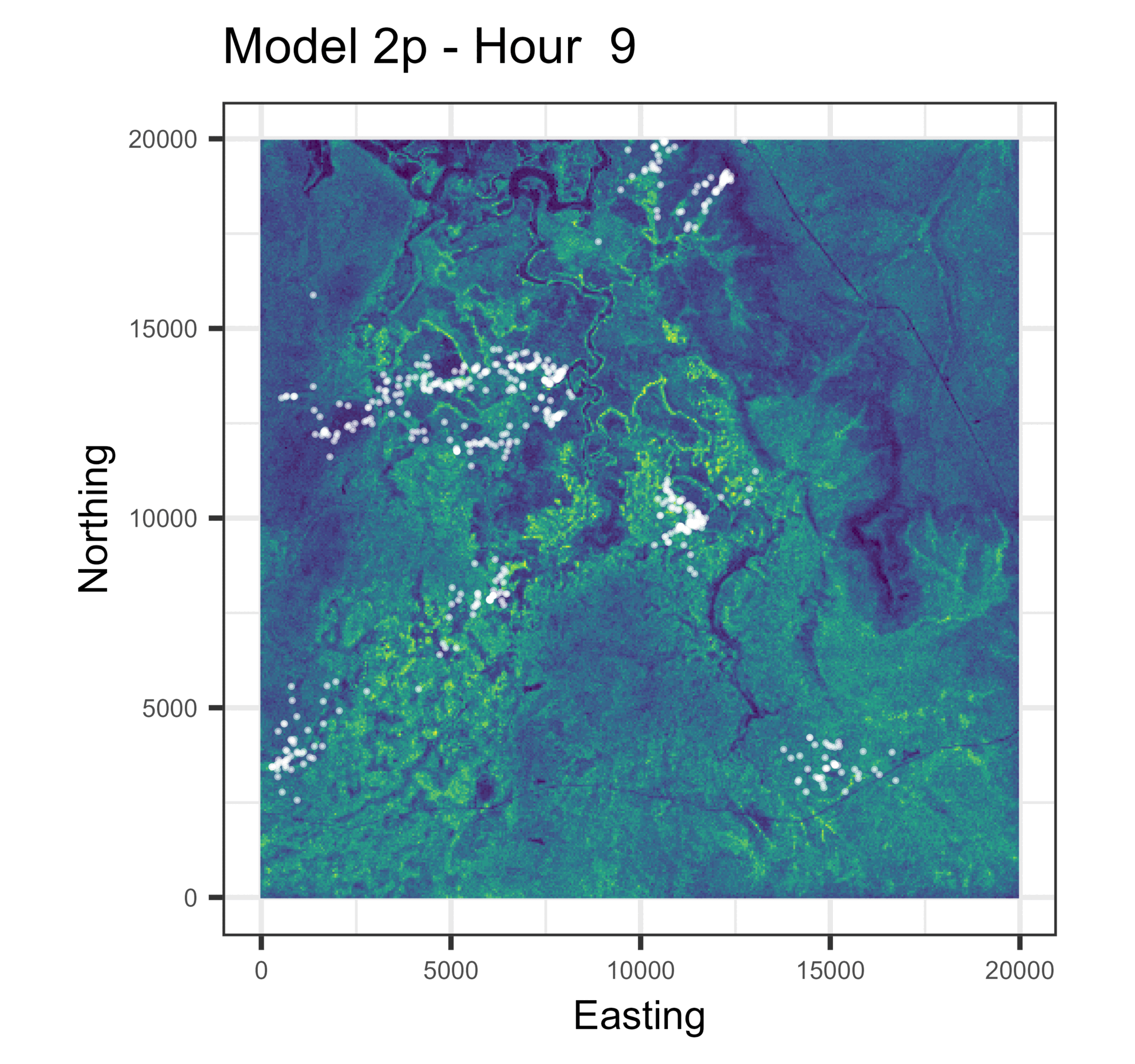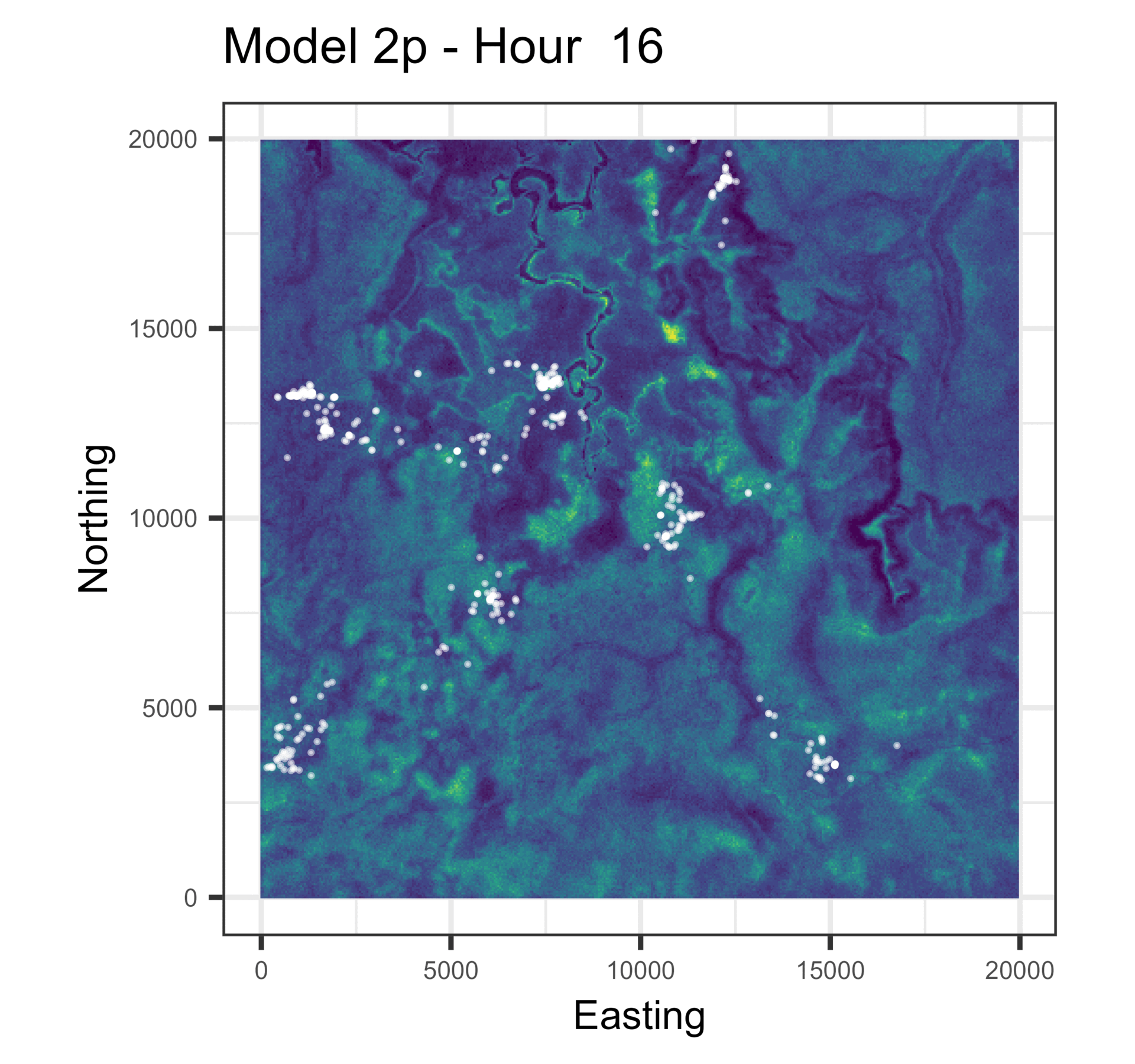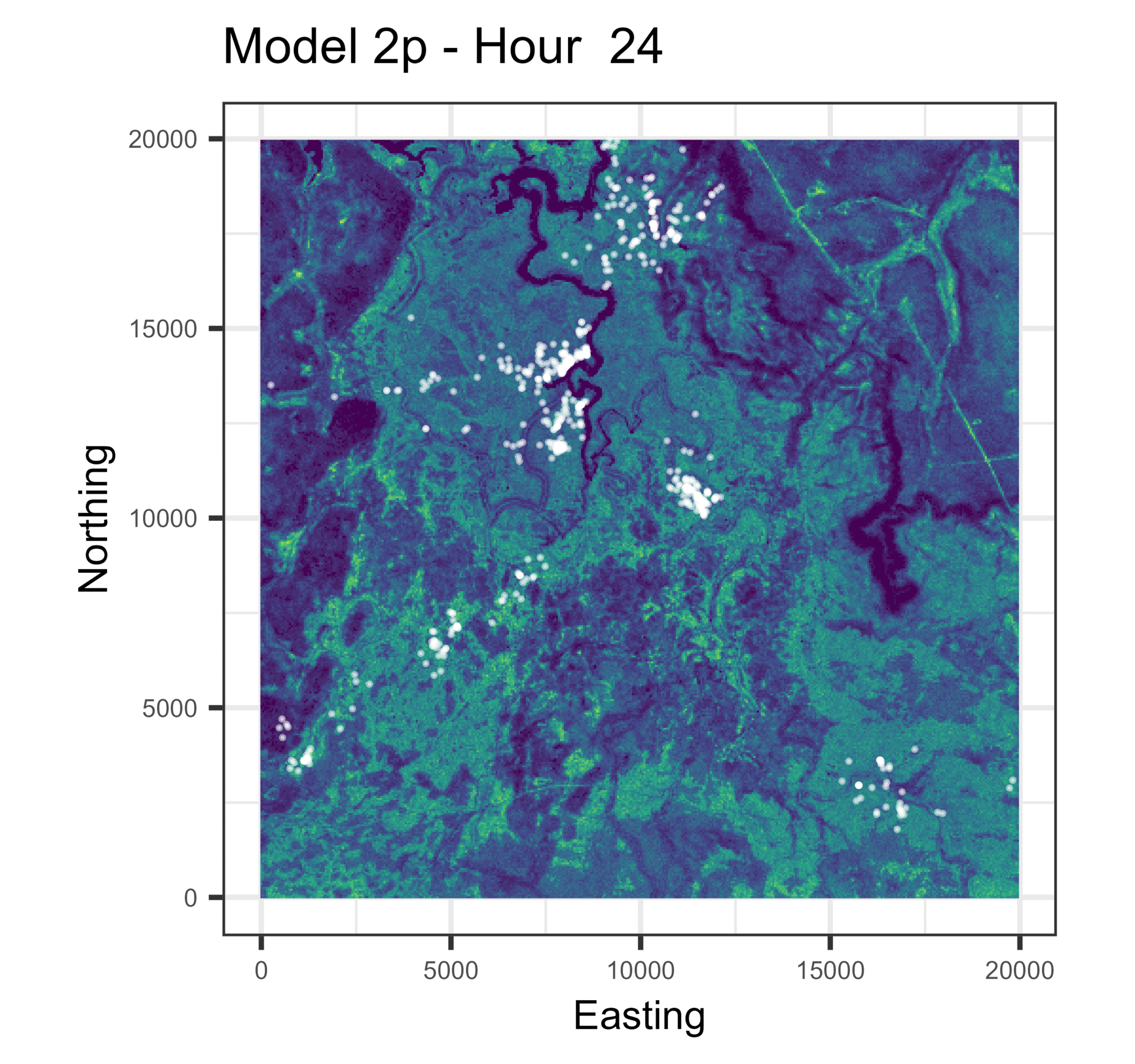
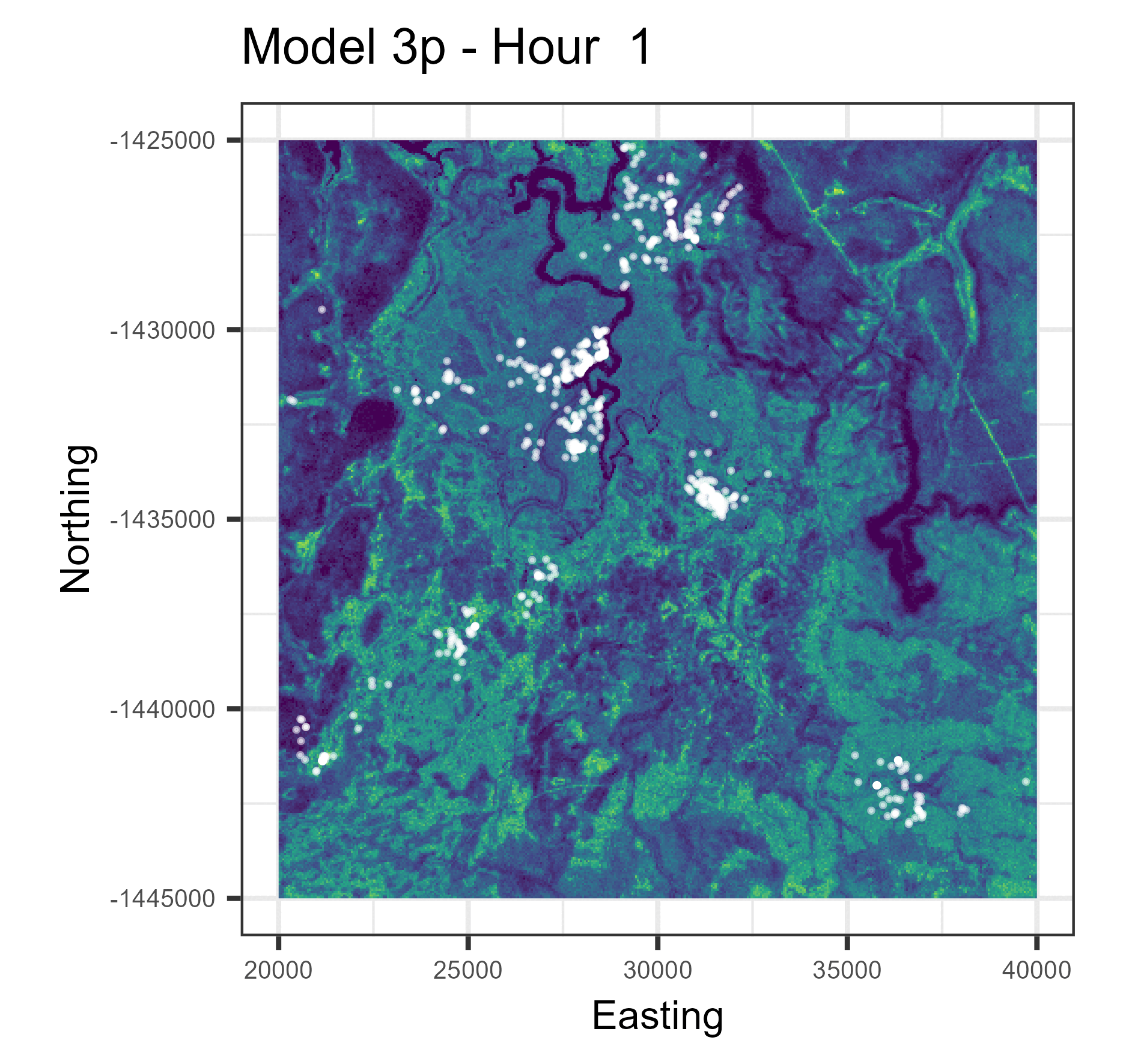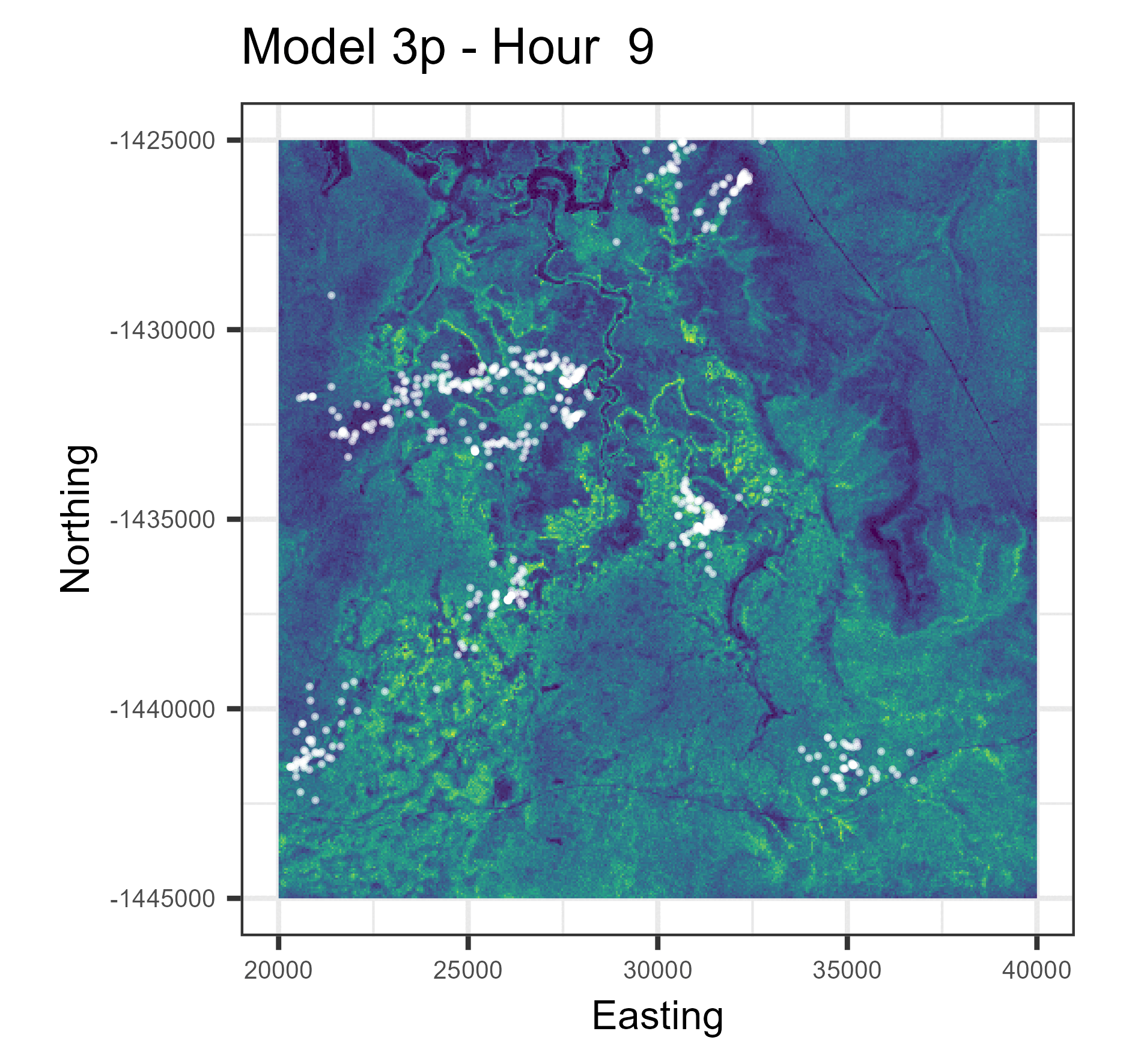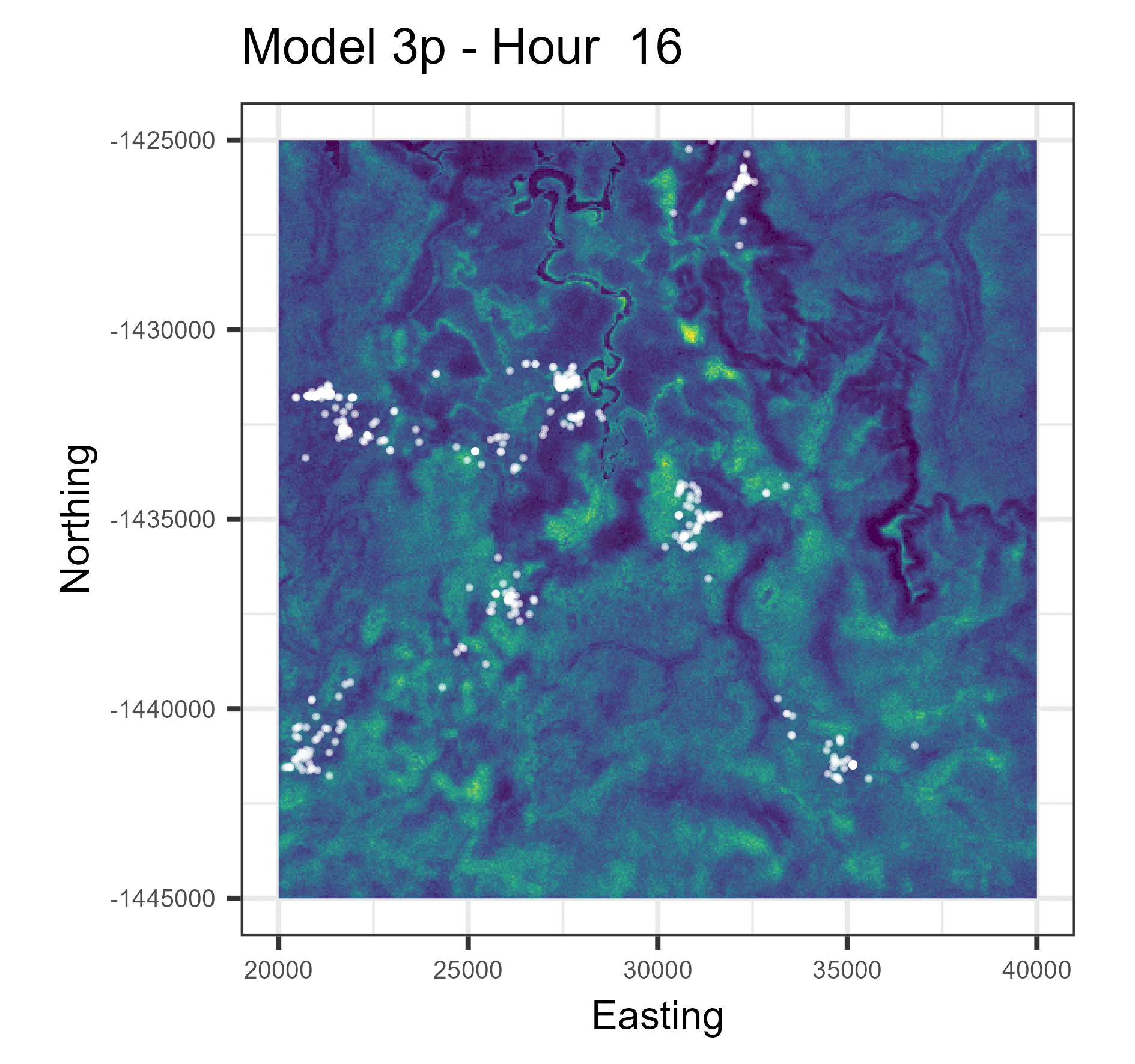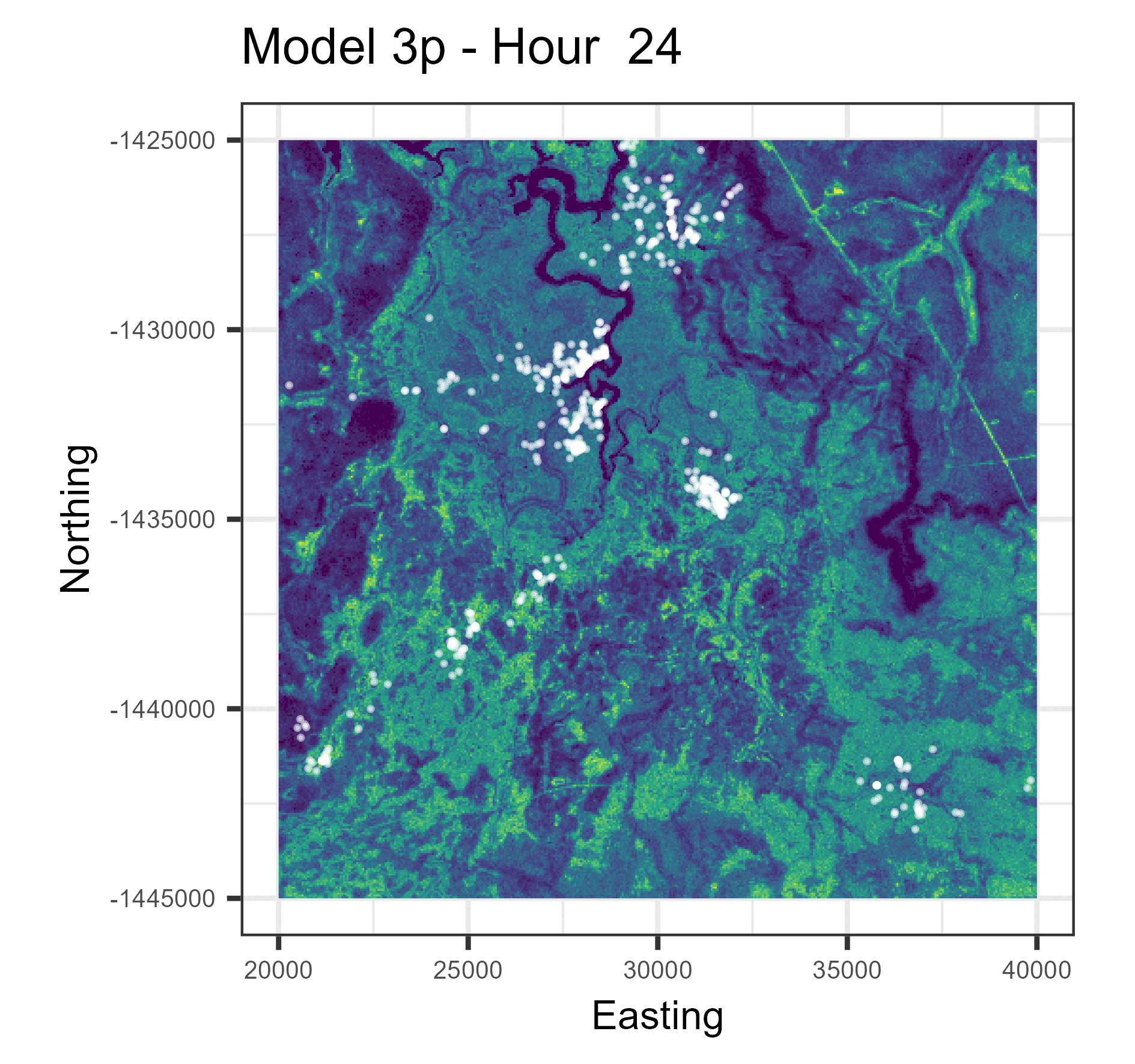
In this paper we used harmonic terms to estimate temporally dynamic coefficients from step selection models, from which we simulated animal movement trajectories. The simulations with temporal dynamics gave informative hourly predictions of expected buffalo distribution (animations below), and also gave more accurate long-term predictions.
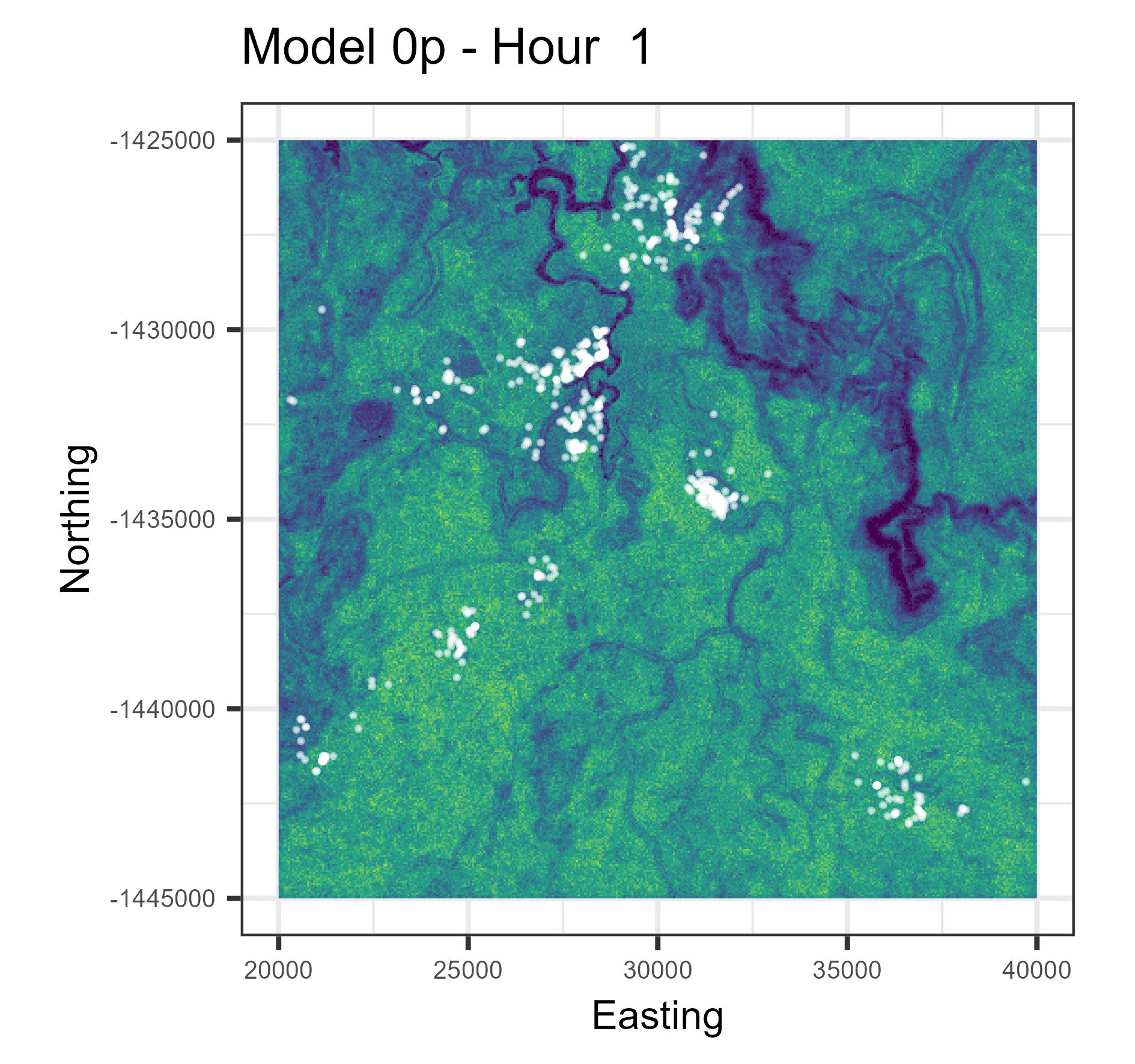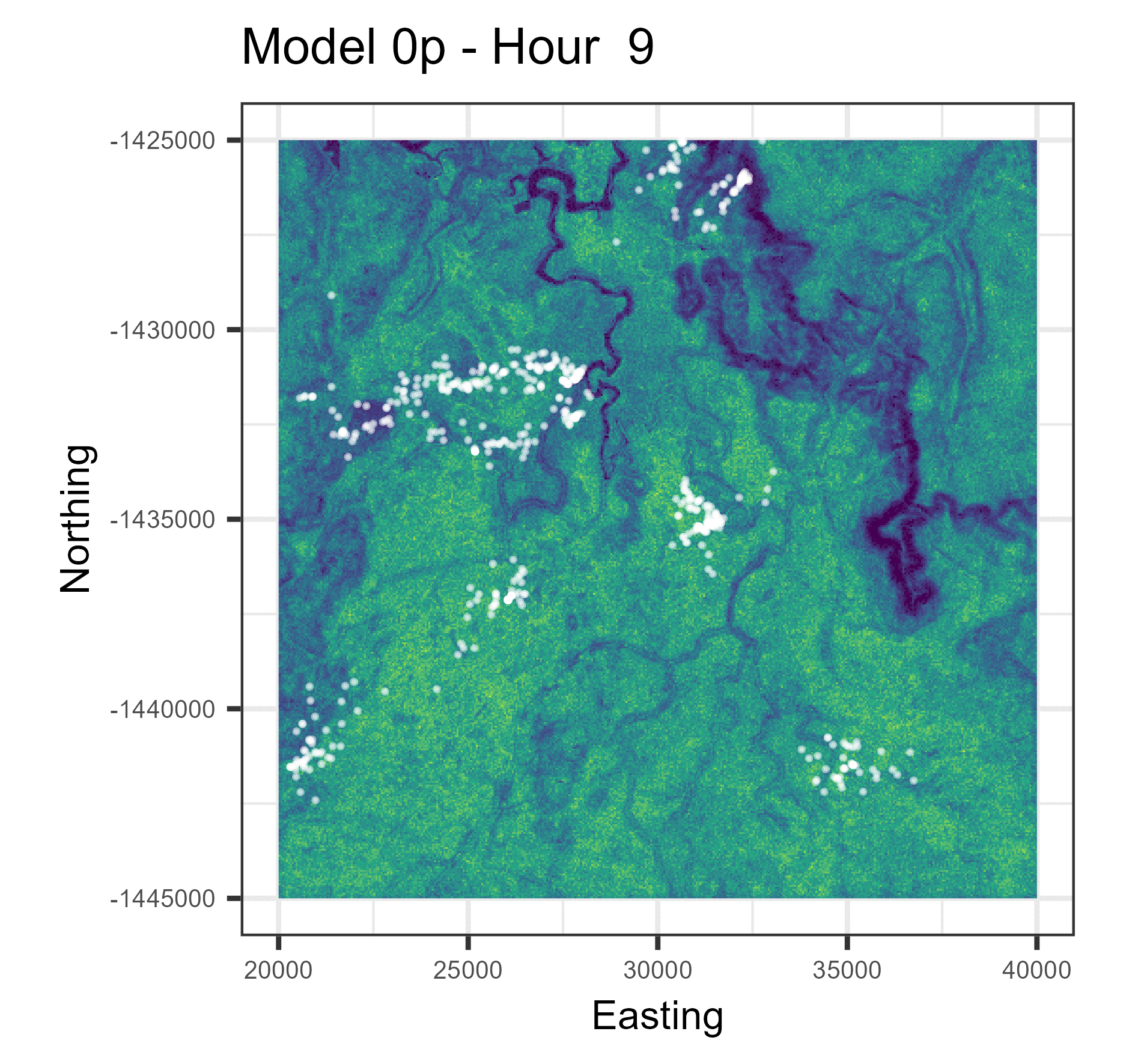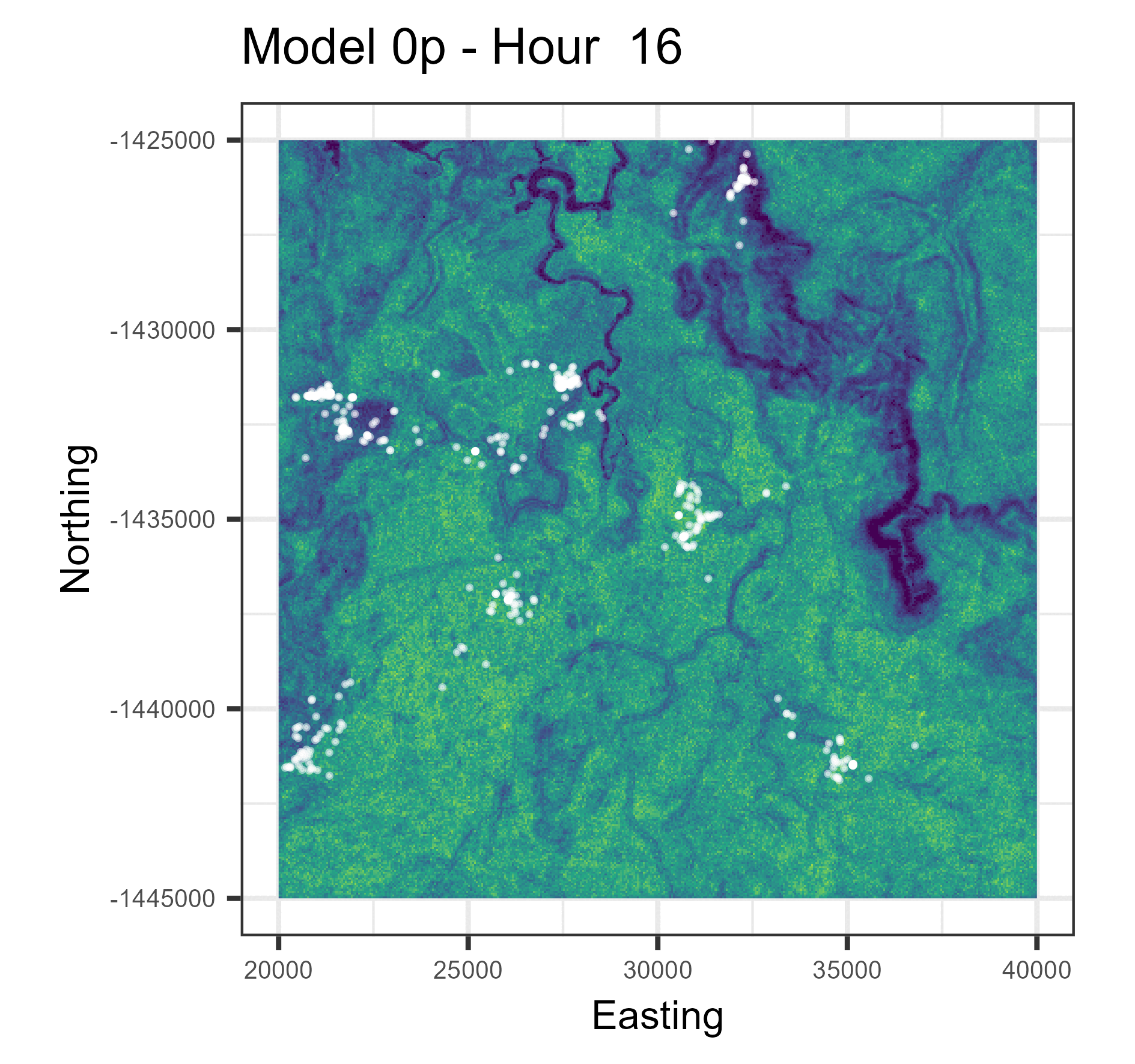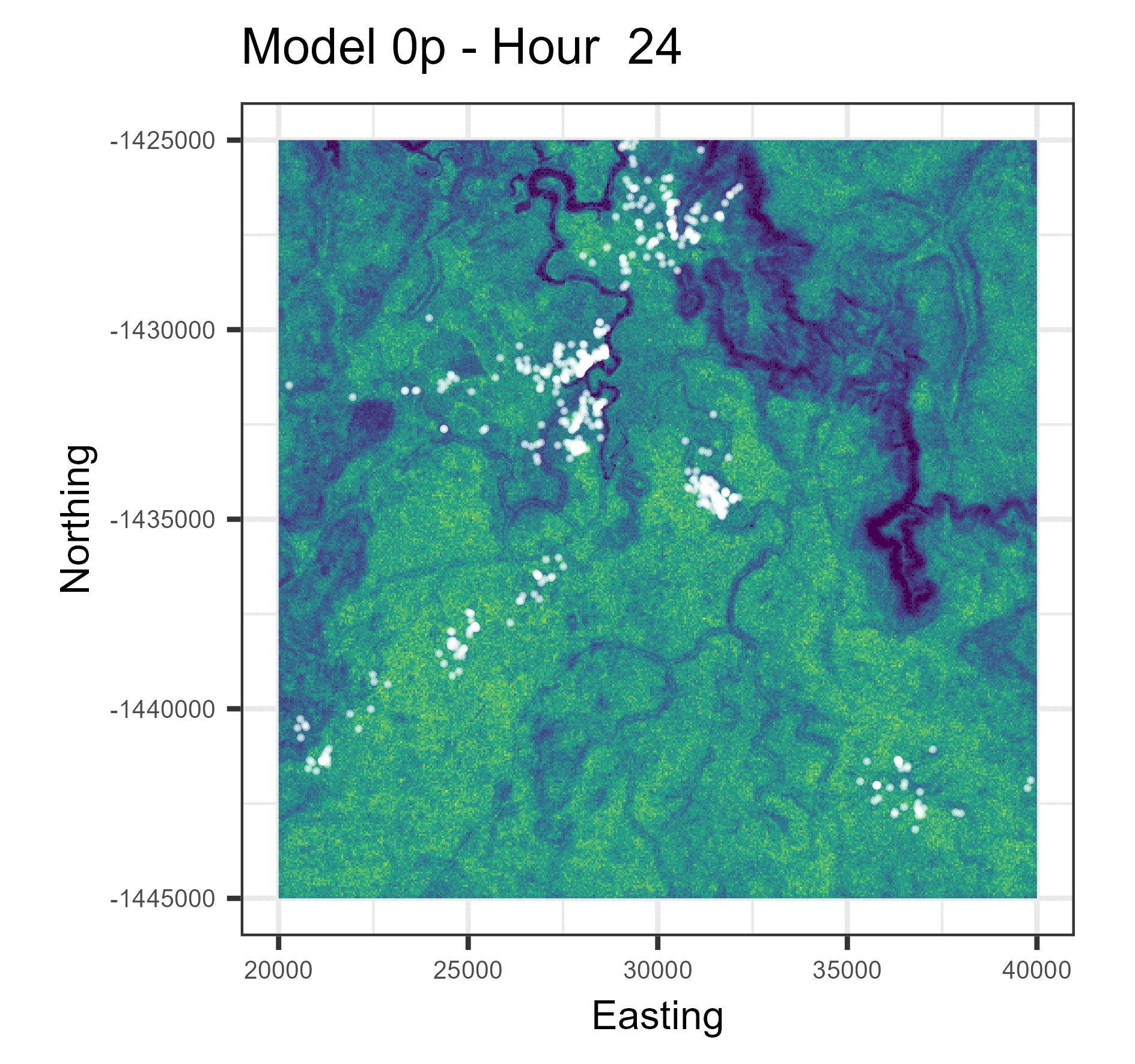
Animations of hourly distributions
The observed buffalo locations for a given hour are shown as the white locations, and the heatmap is the result of running many (dynamic) SSF simulations. There are locations from several individual buffalo in this landscape extent.
Harmonic regression tutorial
We provide a script below is a walkthrough to build intuition around fitting models with harmonic interaction terms (harmonic regression).
DynSSF_Walkthrough_Harmonics_and_selection_surfaces
For more scripts and data, please visit the GitHub repository: GitHub repo: https://github.com/swforrest/dynamic_SSF_sims